VEF Blog

3) Constructions mathématiques

Géode par triangulation
La plupart des géodes sont bâties sur le principe suivant : on part d'un icosaèdre.

 

          

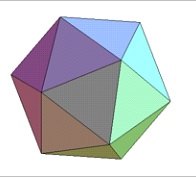
Chacun des sommets de l'icosaèdre est commun à cinq facettes triangulaires, adjacentes deux à deux, et  cinq arêtes (côtés des facettes) partent de chacun de ces sommets.
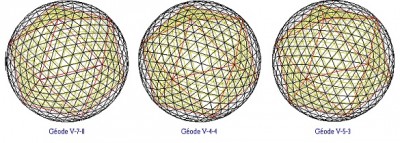
Chaque facette de l'icosaèdre est un triangle équilatéral, que l'on va subdiviser en triangles plus petits qui sont ensuite déformés (par projection radiale) pour être amenés sur la sphère circonscrite à l'icosaèdre. Voici trois exemples de géodes, correspondant chacun à une subdivision différente :
 

 

               

 

Dans le premier exemple, on a divisé les arêtes des faces de l'icosaèdre en deux segments. Dans le second, les arêtes ont été divisées en trois. Enfin, dans le dernier, elles ont été divisées en dix segments. C'est d'ailleurs sur ce dernier modèle qu'est bâtie la Géode de la Cité des sciences et de l'industrie de la Villette.
Pour repérer l'emplacement des sommets de l'icosaèdre initial, il suffit de trouver les endroits où 5 petits triangles (au lieu de 6) partagent un même sommet !


Principes de la construction géométrique d'une géode
Les dômes géodésiques sont des structures basées sur la division (partition) des faces d'un polyèdre régulier dont les faces sont constituées de triangles équilatéraux.
Il n'existe que 3 types de polyèdres réguliers possédant de telles faces équilatérales : le tétraèdre régulier (N = 3), l'octaèdre régulier (N = 4) et l'icosaèdre régulier (N = 5), la notation N utilisée ici représentant le nombre de faces (et aussi le nombre d'arêtes) qui partagent un même sommet.
La division des faces est définie par deux paramètres entiers a et b, positifs ou nuls.
Le premier paramètre a doit être strictement positif.
Le second paramètre b peut être nul mais ne doit pas être supérieur à a.

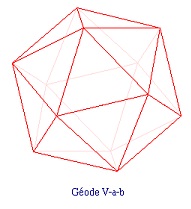
 Une fois choisies les valeurs de N puis de a et de b, la construction du dôme correspondant, que par la suite nous noterons « Géode M-a-b » (notation où le M doit être remplacé par III, IV ou V, selon la valeur en chiffres romains du nombre N), se déroule en 6 étapes, que nous allons expliquer en détail en privilégiant le cas N = 5 (qui correspond à l'immense majorité des géodes) et en l'illustrant dans les 3 cas suivants : a=7,b=0 puis a=4 et b=4 et enfin a=5, b=3 
À partir d'un icosaèdre régulier

Étape n° 1
* On construit un polyèdre régulier (R) correspondant à la valeur de N.

Étape n° 2

* On choisit l'une des faces du polyèdre (R) puis l'une des arêtes de cette face (qui est toujours un triangle équilatéral). Soit AB l'arête choisie et C le sommet opposé à cette arête sur la face choisie.
* On divise alors le segment AB en (a + b) segments de longueur égale et l'on numérote tous les points ainsi définis : le point A reçoit le n° 0, le point suivant le n° 1, le suivant le n° 2, etc. et le dernier, c'est-à-dire le point B, le n° a + b. Soient P0, P1, P2...Pa-1, Pa, Pa+1..., Pa+b  les points ainsi obtenus.
 *On trace ensuite le segment Cpa

 Enfin, on trace tous les segments parallèles à Cpa et passant par chacun des points P0, P1, P2...Pa-1, Pa, Pa+1..., Pa+b  , sans toutefois dépasser les limites de la face ABC.





 Étape n° 3

On répète la même opération en changeant respectivement l'arête AB et le sommet C, en BC et A, puis en CA et B ; on obtient ainsi un triple réseau de segments parallèles et équidistants faisant entre eux des angles de 60° et délimitant donc des petits triangles équilatéraux dont certains (sauf si le paramètre b vaut 0) sont incomplets. Ce sont les sommets de ces petits triangles qui vont servir à construire le dôme géodésique, y compris ceux qui sont situés juste à cheval sur l'une des arêtes de la face ABC.
Bien entendu, il faut répéter les opérations décrites aux étapes 2 et 3 pour toutes les faces du polyèdre (R). Rappelons que le tétraèdre possède 4 faces, l'octaèdre 8 faces et l'icosaèdre 20 faces



Étape n° 4

 Soit O le centre de la sphère (S) circonscrite au polyèdre (R). Par la projection radiale de centre O, on projette sur la sphère (S) l'ensemble des réseaux obtenus ou, plus exactement, les sommets des petits triangles équilatéraux qu'aux étapes n° 2 et 3, on a obtenus sur chacune des faces de (R).






Étape n° 5

 

 

 Pour former les arêtes du dôme géodésique V-a-b, on doit relier les divers sommets obtenus à l’étape précédente : toutefois, il ne faut relier entre eux que les sommets qui sont la projection de sommets appartenant à un même petit triangle équilatéral (voir étape n° 3).







Étape n° 6

Les arêtes obtenues à l'étape précédente forment des triangles sphériques, qui sont la projection radiale des petits triangles équilatéraux résultant de la division des faces du polyèdre initial (R).
 Pour achever le tracé de la géode V-a-b, il suffit d'effacer la trace de toutes les opérations effectuées aux étapes n° 1 à 4 : les sommets des triangles sphériques restants sont les sommets de la géode ; ces sommets, reliés deux à deux, dessinent l'ensemble des sommets et des faces de la géode V-a-b.